CPU architecture

2022-01-27

Steven Whitaker

Introduction

Digital logic is any analysis using a digital signal: a 0 or a 1. There's nothing more to it. It is the most basic digital analysis.

Basic digital logic

There are a few building blocks for digital logic:

AND gate
OR gate
NOT gate

If there are two inputs, A, B, then the output, Y is mapped for each as follows:

---------------------------------
|  A  |  B  ||  AND Y  |  OR Y  |
+-----+-----++---------+--------+
|  0  |  0  ||    0    |   0    |
+-----+-----++---------+--------+
|  0  |  1  ||    0    |   1    |
+-----+-----++---------+--------+
|  1  |  0  ||    0    |   1    |
+-----+-----++---------+--------+
|  1  |  1  ||    1    |   1    |
---------------------------------

So, it's the same idea in C using & and | in your if statements. The NOT gate, ! is the same in C. How are these built? That is in the hardware meeting.

Any digital output is found using these 3 gates. A NAND gate is NOT+AND. An XOR gate is AND( NOT( AND(A, B) ), OR(A, B) ). I'd just look up a picture of an XOR gate for this. Simply look up "xor gate" and you'll find a good picture of this circuit.

Example: multiplexer and decoder

Suppose you want to have one or another input signal passed directly through to the output. The psuedo-code is an if statement

if C == 0, then
    Y = A
else,
    Y = B
endif

In C, we can use a ternary operator:

Y = C ? A : B;

This is why ternary operators exist, because "if statements" don't actually exist in hardware. It just becomes a complicated ternary operator setup. Here's a 1-bit multiplexer, where you only have A_0 and B_0 passed directly into Y_0 depending on a C value.

   C --+
       |
     +---+
     |    \
A ---| 0   |
     |     |--- Y
B ---| 1   |
     |    /
     +---+

=================================================

                   A
                   |    +-----+
                   +----|  2  |
         +-----+        | AND |---+ 
C ---+---| NOT |--------|     |   |   +----+
     |   +-----+        +-----+   +---|    |
     |                                | OR |--- Y
     |                  +-----+   +---|    |
     +------------------|  1  |   |   +----+
                        | AND |---+
                   +----|     |
                   |    +-----+
                   B

When C = 0, the AND1 becomes "shut off" because C is forcing the output of AND1 = 0 always. Additionally, the AND2 becomes "active" because the output of AND2 is now fully dependent on A.

When C = 1, the AND2 becomes "shut off" because C is forcing the output of AND2 = 0 always. Additionally, the AND1 becomes "active" because the output of AND1 is now fully dependent on B.

Let's now look at a decoder. The pseudo-code for a decoder is:

if C = 0, then
    Y_0 = 1
    Y_1 = 0
else
    Y_0 = 0
    Y_1 = 1
endif

There's a strange similarity here to a bit of code in C:

output = Y[C];

We are indexing into an array with a decoder. If I want the Nth array input, I need to set it somehow. Rather than a direct pass through, I can use a decoder to reduce the dimensionality from 2^N lines to N lines. Since the 1-bit example is stupid, here's a 2-bit example, where we have C_0, C_1 to index into Y_0, Y_1, Y_2, Y_3. Rather than drawing another diagram (since it'll be disgusting real quick), I can just show the code very easily.

Y_0 = AND( NOT(C_1), NOT(C_0) )
Y_1 = AND( NOT(C_1),     C_0  )
Y_2 = AND(     C_0 , NOT(C_0) )
Y_3 = AND(     C_0 ,     C_0  )

Without a decoder, imagine that you need a same-sized array to index into the array itself. So, you have 10,000 floating point numbers. You'd need a 10,000 digit number to index into it! How silly, you'd only need a 14-bit number to index into the array using a decoder.

Advanced digital logic

Flip flops

There are some strange configurations that can be made using digital logic that isn't just AND/OR gates. Our digital logic class talks about flip flops, so let's discuss an RS flip flop:

S  - Setter
R  - Reseter
Q  - Output
Q* - Not used, but I need to name it something.

          +------+
S --------|  0   |
          | NAND |------+--- Q
     +----|      |      |
     |    +------+      |
     |                  |
     +---------------+  |
                     |  |
     +---------------|--+
     |               |
     |    +------+   |
     +----|  1   |   |
          | NAND |---+------ Q*
R --------|      |
          +------+

It looks a little complicated, so let's step through an instance of this where Q = 1 and Q* = 0 are the initialized values. If we have S = 1, then let's see what happens:

Q* = 1 and S = 1, so NAND0(S, Q*) = NAND0(1, 1) = 0. So, Q = 0 now.
Now, Q = 0, so let's look at NAND1 because Q is one of the inputs. NAND1(R, Q) = NAND1(R, 0) = 1. No matter what R is, Q* will always be 1.
Let's double check to see what happens with NAND0 now that Q* has changed! NAND0(S, Q*) = NAND0(0, 1) = 0. Nothing will change, we're stable!

So, if we have the setter equal to 1, we force Q = 0 always. This means we're setting the output to always be 0, no matter what the value was before.

One very interesting output is if you happen to have S=1, R=1, let's see this now (Q = 1 and Q* = 0):

Q* = 0 and S = 1, so NAND0(S, Q*) = NAND0(1, 0) = 0. So, Q = 0 now.
NAND1(R, Q) = NAND1(1, 0) = 1. So, Q* = 1 now.
NAND0(S, Q*) = NAND0(1, 1) = 1. So, Q = 1 now.
NAND1(R, Q) = NAND1(1, 1) = 0. So, Q* = 0 now.

We never stop! We just keep going back and forth. In the best case scenario, you'd get an undefined output. In the worst case scenario (and much, much more likely), you've freaked out your power supply by toggling so fast, it fries or you instantly drain your battery. You cannot have S=1, R=1 or else you will break things.

Go through the same steps for each combination (S=0, R=0, and S=0, R=1) and try to figure out why R is called a "reset" value.

In fact, an SR latch can be seen as a register. If S=0, R=0, then the output will be whatever is stored in the Q line. This is reading from the register. If S=1, R=0, then the Q line will be set to 1. This writes a 1 to this register bit. If S=0, R=1, then the Q line will be set to 0. This writes a 0 to this register bit. For a 64-bit register, you just stack 64 of these suckers together.

CPU architecture components

A CPU consists of executing a series of instructions. Adding two numbers, loading/storing a value from/to disk, or jumping to a new instruction pointer.

The instruction is split to two points:

What are you doing?
On what data are you doing this?

The "what are you doing" is called a "opcode", it's part of the instruction that does the OPeration on the CODE.

The "on what data" is called the "operands", it's just a list of what values are being done on the data.

Let's just focus on the arithmetic logic unit (ALU) right nowsince it's a simple set up and easily steps you into the architecture.

ALU

The ALU is used to do the operations on registers. For example, adding, subtracting, and, or, not, xor, etc.

Let's make an ALU in C:

switch (OPCODE){
    case ALU_ADD: Y = A + B; break;
    case ALU_SUB: Y = A - B; break;
    case ALU_NOT: Y = !A; break;
    case ALU_AND: Y = A & B; break;
    case ALU_OR:  Y = A | B; break;
}
...

Yup, an ALU is a case statement. The ALU all passes the data into a single output, Y, so we can use a multiplexer to make sure the correct output is mapped to the correct operation.

                        OPCODE ---+
                                  |
      +-------------+      +-------------+
A --- |             |      |             |          
      |  ALU STUFF  | ==== | MULTIPLEXER | --- Y
B --- |             |      |             |
      +-------------+      +-------------+

============= ALU STUFF ==============

A     B
|     |     +-------+
+---- | ----|       |---------- (A+B)
|     +-----| ADDER |
|     |     +-------+
|     |     +------------+
+-----|-----|            |----- (A-B)
|     +-----| SUBTRACTOR | 
|     |     +------------+
.     .
.     .
.     .

Now, we can really get into the meat and potatoes of a CPU, but it will get messy very quickly, because after this, it's fully customizable. You can set it up any way you want, and many CPUs are very, very different. For example, the 6502 has three general purpose registers, and MIPS has around 16. They're all optimized for their own reason.

Registers

You may have heard of "special registers" before, but the only special thing about them is that you typically don't edit them; the CPU itself will be modifying them, so you really only want to read from them. The main special register that's important is the program register: what instruction is being loaded next?

General purpose registers are the ones where you operate on. So, image it's the A, B, and Y pipes I've drawn above.

Instructions

A normal (RISC) instruction set architecture (ISA) normally works like the following:

Register operations:
+----+-----------+-----------+-----------+-----+
| op | operand 1 | operand 2 | operand 3 | ALU |
+----+-----------+-----------+-----------+-----+

Jump operations:
+----+------+---------------------------+
| op | jump |       memory address      |
+----+------+---------------------------+

Loading + storing data:
+----+-------+--------------------------+
| op | LD/SD |      disk address        |
+----+-------+--------------------------+

op is the opcode. What's happening? Are we going to work on registers? Are we going to jump the address pointer? Are we going to load data?
operand 1, 2, 3 are the three registers that will be pulled into the ALU to have operations done. For MIPS, op1=A, op2=B, op3=Y.
jump is the type of jump to be done, say do we jump when two numbers are equal, do we jump when one is greater than another?
LD/SD is load data, store data

NOTE: If you want to know more about this, Harvey Mudd's class is much much better than Michigan Tech's (we use their textbook). David Harris is a fantastic professor for an introduction to CPU design. I'll only be talking about MIPS R-instructions and load instructions. Advanced topics like strategies to mapping out the operations properly, are described in Soner's CS4431 class, specifically the lecture on ISAs (currently, Lecture 2, slides 22+).

CPU

Now, we can dissect this block diagram. There's a bit extra, side things, that are required to clean things up for a CPU, but I'll just focus on the main parts.

RISCV Figure

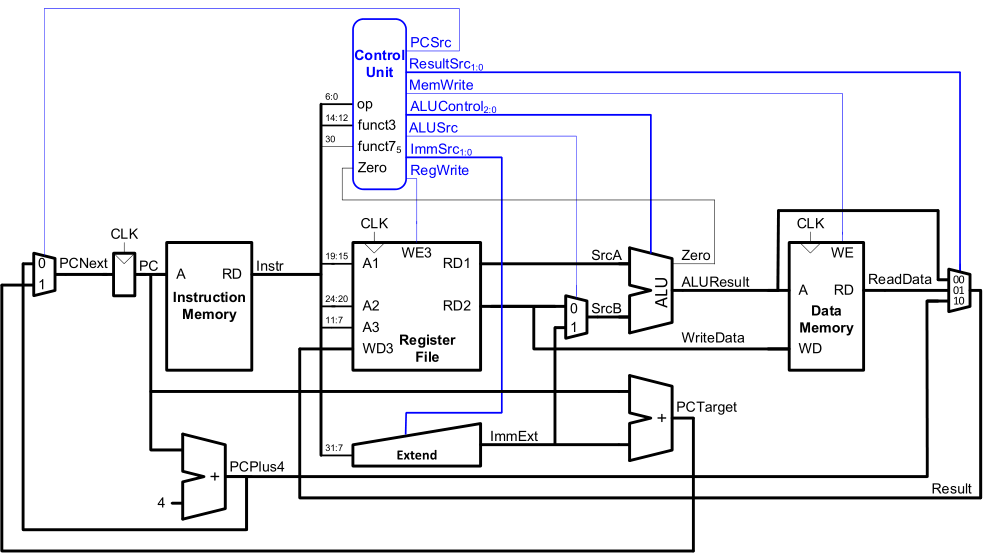
The instruction memory is your ROM, the program that you want to run. There's no real CPU stuff going on here; this is your binary file.
The register file is a bunch of registers. The instruction found in the instruction memory tells you which registers are mapped. There's no real CPU stuff going on here; it's just your variables.
The control unit figures out the output of the instruction. This is the case statement in the ALU wrapper.
The ALU is the operation unit.
Data memory is RAM in this case, but it could also be thought of as disk storage.

Stepping through instructions

R2 = R0 + R1

We are adding registers R0 and R1 and writing the output into register R2.

The instruction is found in the instruction memory. The program counter (PC) "finds" it by indexing into the instruction memory using a very, very big decoder. We can immediately increase the PC to the next instruction and wait.
The instruction's operands say that R0 and R1 are the inputs and R2 is the output, so A1 = R0, A2 = R1, A3 = R2.
The control unit determines (using digital logic gates on the specific bits on the instruction) that we want the output to have: the WE3 flag on the register, since we want to write to A3. The control unit also determines we want to use the ALU to add A1 and A2.
The ALU adds the two numbers together.
The Result is ALUResult and is written to the A3 register, R2.
LD R3 0x0155

We are loading whatever data is in 0x0155 into the R3 register.

The instruction is found in the instruction memory. The program counter (PC) "finds" it by indexing into the instruction memory using a very, very big decoder. We can immediately increase the PC to the next instruction and wait.
This gets confusing, because random bits will be set for A1 and A2, because the register file has no idea what is actually on the instruction: it's a dumb register pool. But, because we aren't doing anything with these, it doesn't matter! We just need A3 = R3 and then move on.
The control unit tells us we want to read from memory and have the Result be whatever is read from memory.
The ALU is "not used". A1 and A2 are going to be passed through the ALU, but A1 and A2 aren't set, and the far-right multiplexer ignores this output anyway. So, it doesn't matter.
Result is ReadData and is written to the A3 register, R3.